LSTMs and Music Generation
This is a project I started after working through the fascinating and thoughtful MIT 6.S191 - Introduction to Deep Learning.
Have you ever wanted a computer to generate an endless stream of original music in the style of your favorite musician or composer? Well it's EZPZ with neural networks!
A recurrent neural network (RNN) is a powerful network that makes use of a hidden state. In short, this allows a network to retain information about previous input. This has all sorts of useful applications, for example predictive text generation; often the meaning of a sentence can only be understood by connecting words that appear far apart.
An LSTM (long short term memory) is a particular type of RNN that is adept at figuring out long-term dependencies. I won't go into depth, but its structure allows for efficient backprobagation throughout many timesteps thanks to the top arrow flowing from left to right in the diagram below.
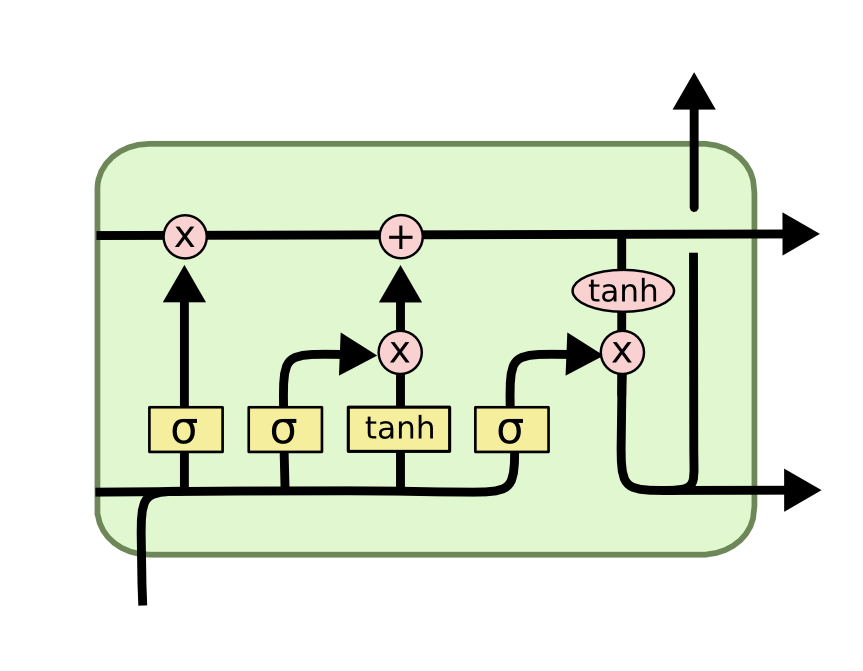
The first lab of MIT 6.S191 has a music generation component making use of LSTMs, but I felt the abc music notation they used to be a bit limiting. I thought MIDI would be a more natural and flexible input.
I found out that people had previously trained LSTMs to take in and output MIDI (e.g. here and here) but these projects focused purely on tone generation and completely ignore rhythm. That is, these networks generate an endless stream of notes but any rhythm has to be entered manually.
I looked for simple examples which take into account both rhythm and pitch, but couldn't find anything that fit the bill. I found some scholarly work that generates Chopin mazurkas, but here they use a fixed grid to output the results; notes can only fall on beats 1, 2, or 3. For all practical purposes, this only seems useful for pieces in 3/4. And even then, you're limited to only quarter notes.
An while this fixed grid approach could be generalized, wouldn't it be nice if the neural network could just learn rhythm on its own?
The Plan
The first thing to do is get some MIDI to feed your LSTM. Here, I'm using the music21 library to read in MIDI files and extract the pitch and time at which each note is played (below, pitches are "notes" and rhythms are "offsets")
def get_notes(path):
notes = []
offsets = []
midfs = glob.glob(path)
for midf in midfs:
print('loading: ', midf)
notes_to_parse = None
midi = converter.parse(midf)
try:
s2 = instrument.partitionByInstrument(midi)
notes_to_parse = s2.parts[0].recurse()
except:
notes_to_parse = midi.flat.notes
for element in notes_to_parse:
if isinstance(element, note.Note):
notes.append(str(element.pitch))
offsets.append(float(element.offset))
elif isinstance(element, chord.Chord):
notes.append('.'.join(str(n) for n in element.normalOrder))
offsets.append(float(element.offset))
return notes, offsets
notes, offsets = get_notes(path)
Now rather than the time at which each note is played, let's find the relative spacing between each note. This is the rhythm I'm going to feed into the LSTM
rel_offsets = []
for i in range(len(offsets)-1):
rel_offsets.append(abs(round(offsets[i+1] - offsets[i],3)))
Great. Next, we need to create a unique mapping between each pitch and a number that the neural net can understand.
# create a dictionary mapping each name to a unique integer
pitch_names = sorted(set(notes))
note_to_int = {note:i for i, note in enumerate(pitch_names)}
# create mapping from indices back to note name
int_to_note = np.array(pitch_names)
num_unique_notes = len(pitch_names)
ditto above for the relative offsets. Now we can take all the data we read in and map each pitch and offset to their respective unique integers. This is what is called vectorizing the input.
def vectorize_notes(notes):
vectorized_notes = np.array([note_to_int[note] for note in notes])
return vectorized_notes
vectorized_notes = vectorize_notes(notes)
Again, we do the same for the relative offsets.
In order to actually train our neural network, we'll need to be able to generate batches for it to train on. Let's say my total input was "A B C D E". I want a function that will extract a chunck of this, say "B C D", get the network to guess the next character, and then compare this to the true answer "E". Being careful to shape the batches so that it plays nice with TensorFlow, this gives us something like
def get_batch_notes(vectorized_notes, seq_length, batch_size):
# length of vectorized notes
n = vectorized_notes.shape[0] - 1
# randomly choose starting indices for the examples in training batch
idx = np.random.choice(n - seq_length, batch_size)
# create input and output sequences to feed into neural net
input_batch = [vectorized_notes[i : i+seq_length] for i in idx]
output_batch = [vectorized_notes[i+1 : i+seq_length+1] for i in idx]
x_batch = np.reshape(input_batch, [batch_size, seq_length])
y_batch = np.reshape(output_batch, [batch_size, seq_length])
return x_batch, y_batch
We're ready to build our network! How exciting!
def LSTM(rnn_units):
return tf.keras.layers.LSTM(
rnn_units,
return_sequences=True,
recurrent_initializer='glorot_uniform',
recurrent_activation='sigmoid',
stateful=True,
)
def create_network(vocab_size, embedding_dim, rnn_units, batch_size):
model = models.Sequential()
model.add(layers.Embedding(vocab_size, embedding_dim, batch_input_shape=[batch_size, None]))
model.add(LSTM(rnn_units))
model.add(layers.Dropout(0.2))
model.add(LSTM(rnn_units))
model.add(layers.Dropout(0.2))
model.add(LSTM(rnn_units))
model.add(layers.Dense(vocab_size))
return model
Of course at this point, we could ask the network to spit out as many notes and offsets as we want. But we'd only have ourselves to blame for the resulting cacophony. We should probably go through some training.
Let's set our loss function
def compute_loss(labels, logits):
loss = tf.keras.losses.sparse_categorical_crossentropy(labels, logits, from_logits=True)
return loss
And we're off!
model_notes = create_network(num_unique_notes, embedding_dim, rnn_units, batch_size)
optimizer = tf.keras.optimizers.Adam(learning_rate)
@tf.function
def train_step(x, y):
# Use tf.GradientTape()
with tf.GradientTape() as tape:
y_hat = model_notes(x)
loss = compute_loss(y, y_hat)
# Compute the gradients
grads = tape.gradient(loss, model_notes.trainable_variables) # TODO
# Apply the gradients
optimizer.apply_gradients(zip(grads, model_notes.trainable_variables))
return loss
# TRAIN~!
history = []
if hasattr(tqdm, '_instances'): tqdm._instances.clear() # clear if it exists
for iter in tqdm(range(num_training_iterations)):
# Grab a batch and propagate it through the network
# x_batch, y_batch = get_batch(vectorized_notes, seq_length, batch_size)
x_batch, y_batch = get_batch_notes(vectorized_notes, seq_length, batch_size)
loss = train_step(x_batch, y_batch)
# Update the progress bar
history.append(loss.numpy().mean())
# Update the model with the changed weights!
if iter % 100 == 0:
model_notes.save_weights(checkpoint_prefix)
# Save the trained model and the weights
model_notes.save_weights(checkpoint_prefix)
We now need to be able to generate some output and then get it into a readable format.
def generate_notes(model, start_string, generation_length=100):
input_eval = [note_to_int[s] for s in start_string.split()]
input_eval = tf.expand_dims(input_eval,0)
text_generated = []
model.reset_states()
tqdm._instances.clear()
for i in tqdm(range(generation_length)):
predictions = model(input_eval)
# Remove the batch dimension
predictions = tf.squeeze(predictions, 0)
predicted_id = tf.random.categorical(predictions, num_samples=1)[-1,0].numpy()
input_eval = tf.expand_dims([predicted_id], 0)
text_generated.append(int_to_note[predicted_id])
return (start_string + ' '.join(text_generated))
generated_notes = generate_notes(model_notes, start_string=np.random.choice(notes)+ ' ', generation_length=140)
We have our output. Now let's put it back into a midi file for our listening pleasure
def create_midi(generated_text, offsets=None):
default_note_spacing = 0.5
scale = 1 #This makes the song faster or slower
if offsets == None: #If we decide to turn off the rhythm, we have the option
offsets_temp = np.arange(0, len(generated_text), default_note_spacing)
else:
offset = 0
offsets_temp = [float(num)*scale for num in offsets]
offsets_temp = [offsets_temp[i] - min(offsets_temp) for i in range(len(offsets))]
output_notes = []
for i, pattern in enumerate(generated_text):
if ('.' in pattern) or pattern.isdigit():
notes_in_chord = pattern.split('.')
notes = []
for current_note in notes_in_chord:
new_note = note.Note(int(current_note))
new_note.storedInstrument = instrument.Piano()
notes.append(new_note)
new_chord = chord.Chord(notes)
new_chord.offset = offset
output_notes.append(new_chord)
else:
new_note = note.Note(pattern)
new_note.offset = offset
output_notes.append(new_note)
offset = offset + offsets_temp[i]
midi_stream = stream.Stream(output_notes)
return midi_stream
Now the moment of truth. Show me what you got LSTM!
Woah. I don't know about you but I'm pretty impressed. The LSTM sounds almost downright musical at times. While it does go a bit off the rails at times, I really enjoy listening to its creations in modest doses. I'm sure there's oodles more I could do to improve it further. But why don't you give that a try? You can see the Google Colab notebooks I used to make this here
:)